lunes, 13 de marzo de 2017

Bibliografia

Bibliografía

Alvarado, E. P. (19 de 08 de 2012). aliat. Recuperado el 13 de 03 de 2017, de aliat: http://www.aliat.org.mx/BibliotecasDigitales/sistemas/Probabilidad_y_estadistica/Probabilidad_y_estadistica-Parte1.pdf

Devore, J. L. (2008). PROBABILIDAD Y ESTADISTICA PARA INGENIERIA Y CIENCIAS. Mexico, D.F.: EDITEC, S.A.de C.V.

Ramon, J. M. (07 de 06 de 2012). probabilidadyestadisticaitsav. Recuperado el 13 de 03 de 2017, de probabilidadyestadisticaitsav: http://probabilidadyestadisticaitsav.blogspot.mx/2012/05/21-teoria-elemental-de-probabilidad.html

2.7 Teorema de Bayes

2.7 TEOREMA DE BAYES

El Teorema de Bayes, permite calcular una probabilidad de un suceso F, a partir de lo ocurrido en el suceso E. Este tipo de teorema usualmente es aplicable a las áreas de control de calidad, para conocer las probabilidades de defectuosidad o no defectuosidad.

La fórmula de Bayes: suponga que F1, F2,…Fn son n eventos que constituyen una participación de un espacio muestral S. Esto es, los F1 son mutuamente excluyentes y su unión es S, además se supone que E es cualquier evento en S, donde P(E) > 0. . La probabilidad condicional de F1 dado el evento E, ha ocurrido y se expresa por medio de la siguiente fórmula:

Sin embargo, la fórmula de Bayes puede ser difícil de recordar y, por tanto, se menciona de forma sencilla:

Cuando se desarrolla la fórmula de Bayes, se puede apoyar en un árbol de probabilidad, el cual es una representación gráfica que permite visualizar las formas en que se llevan a cabo las agrupaciones de los elementos. Ejemplo: en una micro empresa de ropa se da a maquilar pantalones de mezclilla, dicho negocio cuenta con tres proveedores, el señor Roberto, quien maquila 60%, el señor Juan, 30%, y el resto es producido por el señor José.

Con base en la experiencia, el dueño de la empresa cree que la probabilidad de producir un pantalón defectuoso del señor Roberto es de 4% y las probabilidades correspondientes para el señor Juan y el señor José son 9% y 7%, respectivamente. El día de la entrega se encontró un pantalón defectuoso

¿de qué maquilador es más probable que provenga el pantalón de mezclilla defectuoso?

Primero se realiza un árbol de probabilidad para que se pueda ilustrar los caminos de probabilidad:

Después se sustituye la fórmula:

Solución: se sigue el camino de cada uno de los maquiladores, que sería el nombre del maquilador, y después se multiplica por lo el dato que se quiere conocer, en este caso, el camino defectuoso que le corresponde, y finalmente se divide entre todos los caminos a seguir de los casos defectuosos.

Por tanto, si se quiere conocer la probabilidad de que el pantalón defectuoso provenga del señor Roberto:

Si se quiere conocer la probabilidad que provenga del señor Juan:

Si se quiere conocer la probabilidad que provenga del señor José:

Respuesta: es más probable que el pantalón de mezclilla defectuoso provenga del maquilador Juan, ya que la probabilidad es de 46.55%, mayor que la de los otros maquiladores. (Alvarado, 2012)

2.6 Ley Multiplicativa

2.6 Ley Multiplicativa

Al multiplicar la formula P(B/A) =P( A Ç B)/ P(A) por P( A); obtenemos la siguiente regla multiplicativa, esta es importante porque nos permite calcular la probabilidad de que ocurran dos eventos.

Teorema: si un experimento pueden ocurrir los eventos A y B, entonces P( A Ç B)= P( A) P(B/A). Así la probabilidad de que ocurran A y B es igual a la probabilidad de que ocurra A multiplicada por la probabilidad de que ocurra B, dado que ocurre A.

Ø Si los eventos A y B son dependientes:

Ø Si los eventos A y B son independientes:

Ejemplo: Se selecciona una muestra aleatoria n = 2 de un lote de 100 unidades, se sabe que 98 de los 100 artículos están en buen estado. La muestra se selecciona de manera tal que el primer artículo se observa y se regresa antes de seleccionar el segundo artículo (con reemplazo), a) calcule la probabilidad de que ambos artículos estén en buen estado, b) si la muestra se toma sin reemplazo, calcule la probabilidad de que ambos artículos estén en buen estado.

A: El primer artículo está en buen estado.

B: El segundo artículo está en buen estado.

B) Si la muestra se toma “sin reemplazo” de modo que el primer artículo no se regresa antes de seleccionar el segundo entonces:

(Ramon, 2012)

2.5 Probabilidad Condicional: Dependiente e Independiente

2.5 Probabilidad Condicional: Dependiente e Independiente

Para dos eventos cualesquiera A y B con P(B) 0, la probabilidad condicional de

A dado que B ha ocurrido está definida por:

Ejemplo: Supóngase que de todos los individuos que compran cierta cámara digital, 60% incluye una tarjeta de memoria opcional en su compra, 40% incluyen una batería extra y 30% incluyen tanto una tarjeta como una batería. Considere seleccionar al azar un comprador y sea A {tarjeta de memoria adquirida} y B {batería adquirida}. Entonces P(A) 0.60, P(B) 0.40 y P(ambas adquiridas) P(A B) 0.30. Dado que el individuo seleccionado adquirió una batería extra, la probabilidad de que una tarjeta opcional también sea adquirida es:

Es decir, de todos los que adquieren una batería extra, 75% adquirieron una tarjeta de memoria opcional. Asimismo,

El evento cuya probabilidad se desea podría ser una unión o intersección de otros eventos y lo mismo podría ser cierto del evento condicionante. (Devore, 2008)

Eventos Independientes

Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo.

Dos eventos, A y B, son independientes si la ocurrencia de uno no tiene que ver con la ocurrencia de otro.

Por definición, A es independiente de B si y sólo si:A y B, son independientes si la ocurrencia de uno no tiene que ver con la ocurrencia de otro.

Por definición, A es independiente de B si y sólo si:A es independiente de B si y sólo si:

(PnA)=P(A)P(B)
(Alvarado, 2012)

Eventos dependientes

Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (u otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P (A|B) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.

Se debe tener claro que A|B no es una fracción.

P (A|B) = P(A y B) / P (B) o P (B|A) = P(A y B) / P(A)

Probabilidad Condicional = P(A y B) / P (B) o P (B|A) = P(A y B) / P(A)

Dos eventos son independientes si el resultado del segundo evento no es afectado por el resultado del primer evento. Si A y B son eventos independientes, la probabilidad de que ambos eventos ocurran es el producto de las probabilidades de los eventos individuales.

P(A y B) = P(A) · P(B)

(Alvarado, 2012)

2.4 Probabilidad con Técnicas de Conteo: Axiomas, Teoremas.

2.4 Probabilidad con Técnicas de Conteo: Axiomas, Teoremas.

Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función definida sobre un conjunto de sucesos determine consistentemente sus probabilidades.

Los axiomas de la formulación moderna de la teoría de la probabilidad constituyen una base para deducir a partir de ellas un amplio número de resultados.

La letra P se utiliza para designar la probabilidad de un evento, siendo P(A) la probabilidad de ocurrencia de un evento A en un experimento.

AXIOMA 1

Si A es un evento de S, entonces la probabilidad del evento A es:

0 ≤ P(A) ≤ 1

Como no podemos obtener menos de cero éxitos ni más de n éxitos en n experimentos, la probabilidad de cualquier evento A, se representa mediante un valor que puede variar de 0 a 1.

AXIOMA 2

Si dos eventos son mutuamente excluyentes, la probabilidad de obtener A o B es igual a la probabilidad de obtener A más la probabilidad de obtener B.

P(A ∪ B) = P(A) + P(B)

Excluirse mutuamente quiere decir que A y B no pueden ocurrir simultáneamente en el mismo experimento. Así, la probabilidad de obtener águila o sol en la misma tirada de una moneda será

P(A ∪ B) = P(A) + P(B)

P(A ∪ B) = 1/2 + 1/2 = 1.

En general podemos decir que la suma de las probabilidades de todos los posibles eventos mutuamente excluyentes es igual a 1:

P(A1) + P(A2) + P(A3) + ... + P(An) = 1.

AXIOMA 3

Si A es un evento cualquiera de un experimento aleatorio y A’ es el complemento de A, entonces:

P(A’) = 1 - P(A)

Es decir, la probabilidad de que el evento A no ocurra, es igual a 1 menos la probabilidad de que ocurra.

TEOREMAS

TEOREMA 1

Si f es un evento nulo o vacío, entonces la probabilidad de que ocurra f debe ser cero.

p(f)=0

DEMOSTRACIÓN:

Si sumamos a un evento A cualquiera, como f y A son dos eventos mutuamente excluyentes, entonces p(AfÈ)=p(A) +p(f)=p(A). LQQD

TEOREMA 2

La probabilidad del complemento de A, A^c debe ser, p(A^c)= 1 – p(A)

DEMOSTRACIÓN:

Si el espacio muestral d, se divide en dos eventos mutuamente exclusivos, A y A^c luego d=AÈA^c, por tanto p(d)=p(A) + p(A^c) y como en el axioma dos se afirma que p(d)=1, por tanto, p(A^c)= 1 - p(A) .LQQD

TEOREMA 3

Si un evento A Ì B, entonces la p(A) £ p(B).

DEMOSTRACIÓN:

Si separamos el evento B en dos eventos mutuamente excluyentes, A y B \ A (B menos A), por tanto, B=AÈ(B \ A) y p(B)=p(A) +p(B \ A), luego entonces si p(B \ A)³0 entonces se cumple que p(A)£p(B). LQQD

TEOREMA 4

La p( A \ B )= p(A) – p(AÇB)

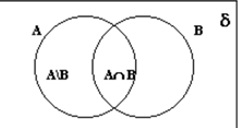
DEMOSTRACIÓN: Si A y B son dos eventos cualquiera, entonces el evento A se puede separar en dos eventos mutuamente excluyentes, (A \ B) y AÇB, por tanto, A=(A \ B)È(AÇB), luego p(A)=p(A \ B) + p(AÇB), entonces, p(A \ B) = p(A) – p(AÇB). LQQD

TEOREMA 5

Para dos eventos A y B, P(AÈB)=p(A) + p(B) – p(AÇB).

DEMOSTRACIÓN: Si AÈB = (A \ B) È B, donde (A \ B) y B son eventos mutuamente excluyentes, por lo que p(A È B) = p(A \ B) + p(B) y del teorema anterior tomamos que p(A \ B) = p(A) – p(AÇB), por tanto, p(AÈB) = p(A) + p(B) – p(AÇB). LQQD.

(Ramon, 2012)

2.3 Probabilidad de Eventos

2.3 Probabilidad de Eventos

Espacio Muestral: El espacio muestral de un experimento denotado por S, es el conjunto de todos los posibles resultados de dicho experimento. (Devore, 2008)

Evento: Un evento es cualquier recopilación (subconjunto) de resultados contenidos en el espacio muestral S. Un evento es simple si consiste en exactamente un resultado y compuesto si consiste en más de un resultado. (Devore, 2008)

Simbología:

1. A, B, C…= conjuntos.

2. a ,b ,c…= elementos de conjuntos

3. U= unión de conjuntos

4. ∩= intersección de conjuntos

5. A‟= complemento de un conjunto

6. / = dado que

7. \ = diferencia

8. <>= diferente de

9. ( )= Conjunto nulo o vacío

10. R= conjunto de los números reales

11. N= conjunto de los números naturales

12. C= conjunto de los números complejos

13. n!= factorial de un numero entero positivo

14. Q= conjunto de los números fraccionarios

15. I= conjunto de los números irracionales

16. c= subconjuntos

17.- { }= llaves.

(Devore, 2008)

Unión: La unión de dos eventos A y B, denotados por A B y leídos “A o B”, es el evento que consiste en todos los resultados que están en A o en B o en ambos eventos (de tal suerte que la unión incluya resultados donde tanto A como B ocurren, así también resultados donde ocurre exactamente uno), es decir, todos los resultados en por lo menos uno de los eventos. (Devore, 2008)

Intersección: La intersección de dos eventos A y B, denotada por A B y leída “A y B”, es el evento que consiste en todos los resultados que están tanto en A como en B. (Devore, 2008)

Diagramas de Venn: Con diagramas de Venn se obtiene una representación pictórica de eventos y manipulaciones con eventos. Para construir un diagrama de Venn, se traza un rectángulo cuyo interior representará el espacio muestral S. En tal caso cualquier evento A se representa como el interior de una curva cerrada (a menudo un círculo) contenido en S. La figura 2.1 muestra ejemplos de diagramas de Venn.

(Devore, 2008)

2.2 Teoría elemental de probabilidad

2.2 Teoría elemental de probabilidad

El Cálculo de Probabilidades se ocupa de estudiar ciertos experimentos que se denominan aleatorios, cuya característica fundamental es la incertidumbre del resultado, esto significa que es imposible predecir los resultados porque hay más de uno posible.

Son ejemplos de experimentos aleatorios: lanzar un dado cinco veces, los instantes de llegadas a un abarrote, etc.

El término de probabilidad es de uso común, así el ente televisivo, el cual nos dirá que es poco probable un cambio brusco de temperatura o un periódico informará que es muy probable que el Real Madrid gane en su campo a Las Palmas.

Este tipo de información es insuficiente cuando se necesita un conocimiento más profundo de un fenómeno aleatorio, Supongamos que una compañía de seguros va a extender una póliza por seguro de vida a un cliente.

Este es el objetivo del Cálculo de Probabilidades, medir probabilidades relacionadas con cierto fenómeno aleatorio dado. Medir significa asignar a cada probabilidad un número determinado, esto nos permitiría obtener un conocimiento más preciso del fenómeno.

Concepto Clásico De Probabilidad:

También conocido como probabilidad a priori. “Si para un evento A hay n resultados igualmente probables, de las cuales f son del tipo que nos interesa, la probabilidad de que ocurra un resultado de este tipo es:

P(a)=f / n

(Ramon, 2012)

2.1.7 Teorema del Binomio

2.1.7 Teorema del Binomio

El teorema del binomio, también llamado binomio de Newton, expresa la enésima potencia de un binomio como un polinomio. El desarrollo del binomio ( a + b)^n posee singular importancia ya que aparece con mucha frecuencia en Matemáticas y posee diversas aplicaciones en otras áreas del conocimiento.

Formula General Del Binomio. Sea un binomio de la forma (a + b). Si a este binomio se le multiplica sucesivamente por sí mismo se obtienen las siguientes potencias:

(Alvarado, 2012)

2.1.6 Diagramas de árbol

2.1.6 Diagramas de árbol

Un diagrama de árbol es una herramienta gráfica que permite enumerar todas las posibles maneras de realizar un conjunto de acciones secuenciales o independientes. El árbol se construye a partir de un nodo, que representa la primera acción a efectuar; de éste se desprenden tantas ramas como maneras diferentes se pueda realizar esa acción; en las terminales de cada rama se dibujan otros nodos, que representan la segunda acción a efectuar y de los que se desprenden tantas ramas como maneras lógicas diferentes pueda realizarse esa segunda acción, considerando la manera en que se realiza la primera. Y así, sucesivamente.

Ejemplo: Considere el experimento consistente en lanzar una moneda tres veces consecutivas y observar, cada vez, la cara que queda hacia arriba. La primera vez que se lanza la moneda, la cara que queda hacia arriba puede ser águila o sol; la segunda vez que se lanza, también la cara que queda hacia arriba puede ser águila o sol, sin importar lo que haya caído la primera vez; lo mismo puede ocurrir la tercera vez que se lanza la moneda. Entonces, el diagrama de árbol correspondiente es:

El número de maneras en que puede caer la moneda tres veces consecutivas es: 2´2´2 = 8

(Alvarado, 2012)

2.1.5 Combinaciones

2.1.5 Combinaciones

La combinación se da sin importar el orden de r objetos sin repetición, seleccionados de entre n objetos tomados de r en r; las combinaciones se anotan con la nomenclatura nCr. Por tanto, el número de combinaciones de n objetos tomados de r en r está dado por:

Ejemplo: En el departamento de una empresa hay 20 trabajadores, quienes deben cubrir una guardia el fin de semana por lo que se formará un grupo de guardia el día sábado conformado por cuatro trabajadores.

¿Cuántos grupos diferentes de 4 miembros son posibles?

Solución: en este ejemplo, el orden de los miembros que conforma el grupo de guardia no es importante, ya que no es necesario determinar cómo van a estar acomodados los integrantes del grupo, por lo tanto: